并发中的同步

条件变量, 哲学家吃饭

条件变量

条件变量用在一个线程需要一直等待一个条件满足后在执行.

比如下面这段代码就是等待count==n满足之后再继续执行.

即使用上了互斥锁, 不用自旋锁, 也是有个类似自旋的过程的:

retry:
    mutex_lock(&lk);
    if (count == n) {
      mutex_unlock(&lk);
      goto retry;
    }

只不过, 这个自旋没有自旋锁那么暴力, 他是更大层面上的自旋:

自旋锁是在上锁的时候, 也就是mutex_lock的时候去自旋, 尝试上锁, 无法上锁就继续自旋.
这个自旋是上锁之后判断条件是否满足, 如果没有条件不能满足就解锁.
这个自旋是有条件的, 注意因为mutex他是维护了一个waiter序列, lock失败后这个线程会阻塞, 只有当有人unlock了之后, 这个线程被唤醒了, 才会去尝试这个大自旋.

看起来, 这个锁尝试自旋的次数并不是很多, 因为只有有人unlock之后他才会自旋.

但是, 一个mutex可能管理了很多个变量, 这个锁可能会非常大, 很有可能一个线程lock了之后更改了一些毫不相干的变量, 然后unlock, 就会把这个线程给唤醒, 造成资源浪费.

这样就有条件变量cond, 条件变量必须和mutex一起用, 并且一个cond只能对应一个mutex.

他支持三个api:

wait(cv, mutex), 标记为因为cv而阻塞.
signal/notify(cv), 唤醒一个因为cv而阻塞的线程.
broadcast/notify_all(cv), 换新所有因为cv而阻塞的线程.

正常的使用方法:

// Thread 1
mutex_lock(&mutex);
while (!cond) {
  wait(&cv, &mutex);
}
// 这里, assert(cond)
mutex_unlock(&mutex);

// Other Threads
mutex_lock(&mutex);
// 这里, 做了一些可能会影响到cond的操作
broadcast(&cv);
mutex_unlock(&mutex);

这是个模版, 我之前在用golang写Raft的时候也经常使用这个模版.

下面来具体分析了一下这地方干了啥:

重点在wait, wait我的理解是完成了下面这三个操作:

mutex.unlock()
让这个线程阻塞, 等待被唤醒.
被唤醒后, mutex.lock()

考虑broadcast的语义, 它会让所有卡在第二步的线程全部启动起来, 这样所有的线程就都会去运行第三步, 争抢mutex. 但是这时候一定只有一个线程能够抢到这个锁. 但是这时候就进入到mutex的语义了: 其他线程虽然没抢到mutex, 又进入了阻塞状态, 但是当mutex被释放后, 他们会因为mutex被唤醒, 从而得到lock, 这一步的唤醒跟broadcast其实是没关系的, 只是因为mutex被释放了.

考虑到第二步这个操作, 如果另一个锁mutex2已经被其他线程lock上了, 那实际上第二步跟mutex2.lock的效果是一样的, 如果把第二步换成这个, 那么mutex2.unlock就相当于broadcast唤醒了所有线程. 但是感觉还是会遇到很多问题, 有时间仔细想想这个跟条件变量的关系吧.

信号量啥的感觉没啥讲的, 就不写了.

哲学家吃饭问题

哲学家吃饭这个经典问题, jyy主张大道至简, 一切都用一个大锁来锁住所有人, 让所有人拿起和放下叉子的过程都是串行的, 然后用条件变量:

mutex_lock(&mutex);
while (!(avail[lhs] && avail[rhs])) {
  wait(&cv, &mutex);
}
avail[lhs] = avail[rhs] = false;
mutex_unlock(&mutex);

mutex_lock(&mutex);
avail[lhs] = avail[rhs] = true;
broadcast(&cv);
mutex_unlock(&mutex);

并且jyy主张不要花时间去考虑其他的比较tricky的方法, 他课上也确实没讲.

不过我还是觉得有些方法还是有一些很值得学习的思想在里面的: 比如我在写6.824的时候就意识到, 如果几个线程都需要获取同样的多个锁, 比如几个线程都需要获取锁mutex1和mutex2, 那这些线程在lock这些锁的时候一定要以一个相同的顺序去lock. 比如要么都是先mutex1.lock再mutex2.lock, 要么都是先mutex2.lock再mutex1.lock, 否则这两个线程一定会死锁.

然后我看到了哲学家吃饭问题的这样的解法: 让奇数编号的哲学家都先拿右手的叉子再拿左手的叉子, 偶数编号的相反. 我总感觉这两个的思想是一样的, 就是那种规定了每个锁的优先级, 所有人在加锁的时候都需要按照相同的优先级顺序去加锁.

进一步的, 我深入思考了这个想法, 发现用操作系统那个资源依赖图模型可以说出一些道理: 如果绘制一张图, 图里的每个节点都是一把锁, 那么每个线程的加锁顺序可以用一个这个图上的一组有向边表示. 比如, 两个线程以不同的顺序去加两把锁, 那么这个图就可以表示为:

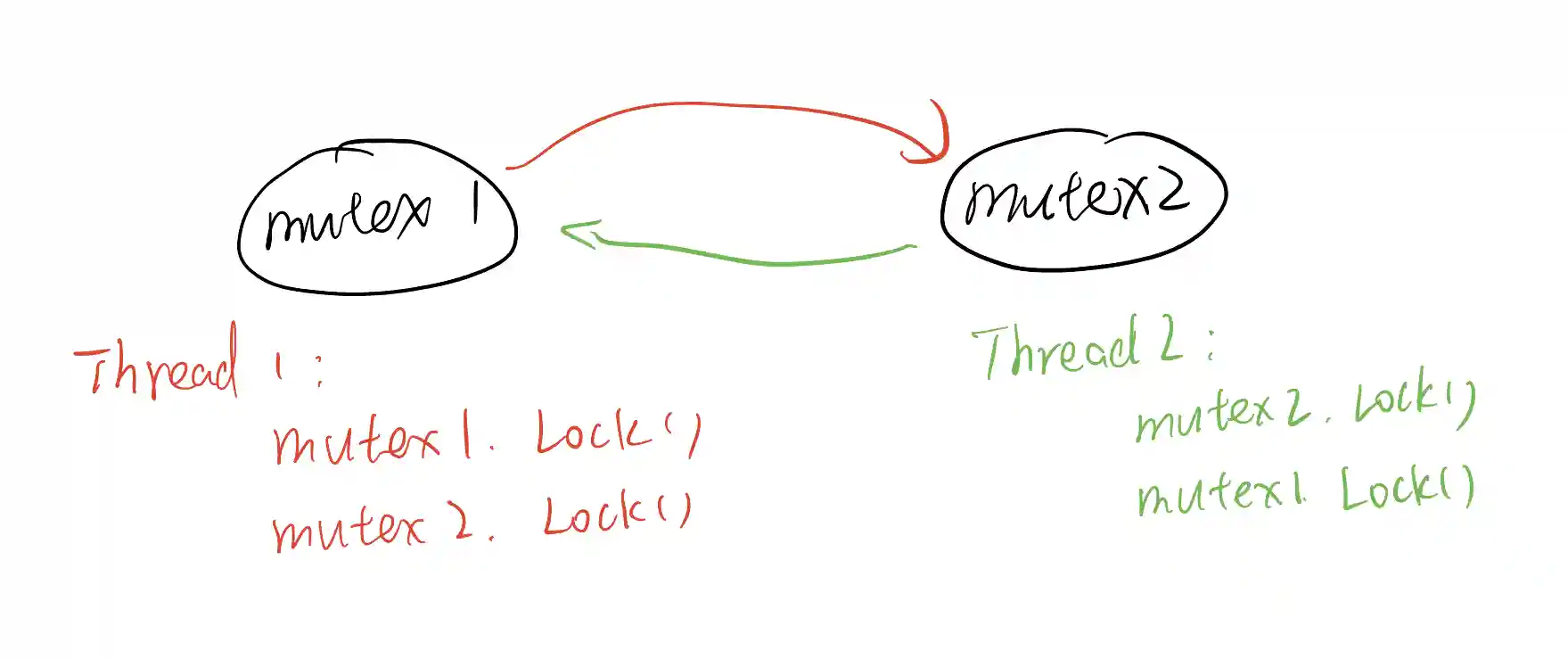
我认为, 死锁可能发生的充分必要条件是这个图上存在一个环. 比如, 考虑下面的这样一个图:

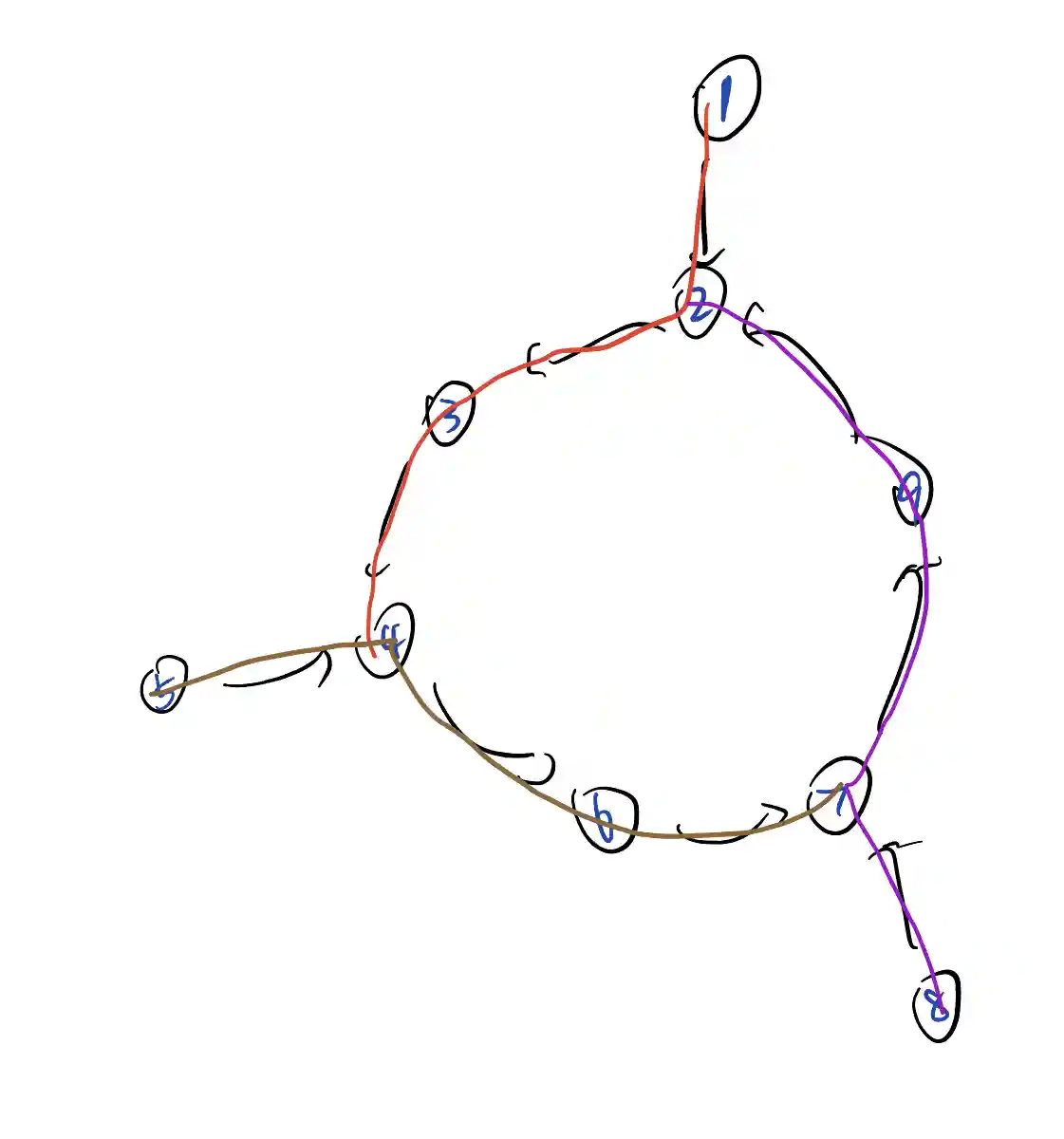
三个线程分别按顺序锁住:

(红色) 1 2 3 4
(棕色) 5 4 6 7
(紫色) 8 7 9 2

这样, 当所有的线程都锁住了他们锁住的第三个锁时, 没有任何一个线程可以锁住最后一个锁, 就死锁了.

如果在哲学家问题中, 让每个人先拿左手边的再拿右手边的, 那这五个锁就会形成一个环. 而我们要做的, 就是控制一些锁加锁的顺序, 让他们永远不可能成环. 比如, 在那个奇偶数的哲学家问题解决方法中, 如果把每个人右手边的叉子标号为这个人的编号, 那么这五个叉子的加锁顺序是这样的:

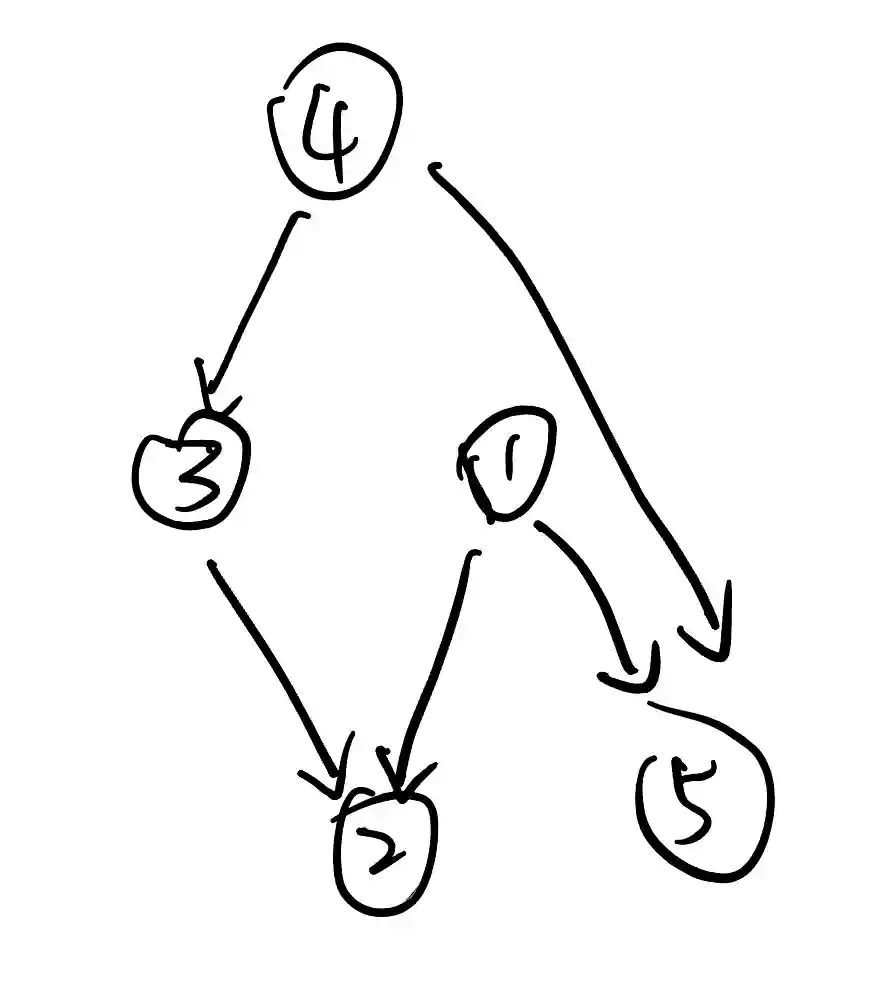
这是一个有向无环图, 在上面无论如何找不到一条成环的路径.

实际上, 这相当于给每个锁设置了一个偏序关系, 这个偏序至少要保证一个线程需要的所有锁都可以互相比较. 这样, 当一个线程需要很多锁时, 就按照这几个锁的偏序关系去加锁, 这样得到的一定是一个有向无环图.

更一般的做法是, 我可以直接给所有的锁一个全序关系, 这样无论任何线程需要多少锁, 只需要按照这个全序关系的顺序去加锁就行. 比如在哲学家吃饭问题中, 完全可以给每个叉子编号之后, 让每个人先拿编号大的再拿编号小的, 这就构造了一个全序关系. 也就是除了第5个哲学家先拿左手再拿右手, 其他的都先拿右手再拿左手, 这样就可以避免死锁.