https://codeforces.com/contest/1623/problem/D
最近在跟队友复健cf, 三个人开黑vp, 感觉状态还是不太行.
这题感觉还挺有意思, 还没过的时候就想如果真的是这样做的一定要写篇文章记录一下, 然而这题是元旦过的, 我现在才开始写, 拖延症晚期了属于是.
前几天刚把自己的win11重装了一遍, 因为感觉莫名其妙的小问题太多了, 也不知道是软件的问题还是系统的问题, tim和qq在打开打开文件的对话框的时候一定闪退. 还有其他小问题我也记不清了, 反正这些问题我都单方面归咎于傻逼win11了. 而对于一个恶人我只需要记住他最恶的一件事就行了, 就是tim和qq在打开打开文件的对话框的时候一定闪退.
重装了系统之后果然tim打开打开文件对话框的时候不闪退了, 我刚为这件事弹冠相庆没多长时间, 他又闪退了. "历史的车轮总是能接受倒退的", 但是当时在写各种大作业, 就没着急换回win10. 但是当我把我计算机图形学作业发给老师之后, 我又发现他又不闪退了, 他的心好难捉摸.
总之我现在就安分地用着这个win11, 去typora官网上下个历史版本, 趁着nodejs还在安装的时候先写个题解.
题目原文:
tmd, 我刚想把这张图发到qq上在保存下来压缩图片, 他又崩了, 麻了.
大概题意就是, 有一个扫地机器人在一个网格, 他有一个初始位置, 然后他每秒可以移动(+1, +1), 但是如果有一个坐标方向上他在墙旁边了, 他的下一步对应坐标的增量就是-1. 这样循环的移动. 有一个垃圾, 他在另一个位置上, 扫地机器人每次移动之前, 都有的概率扫掉对应一行和一列的垃圾. 问期望多长时间他能扫掉这个垃圾.
因为这场比赛第一题是个不带概率的, 每次一定会扫掉垃圾, 就直接把x和y坐标分开看, 看哪个坐标最先到对应的行和列就行. 所以这题我也直接考虑把两个坐标分开看, 确实推出来了一些东西, 我可以得到这个问题在一维上的公式, 但是这样两个一维的问题还是合并不到一个二维问题上, 所以根据经验这时候就需要直接考虑二维问题.
这样的递归求期望题很多都用了一个期望的技巧, 就是一个问题的期望是固定的, 而且这个问题可以化成很多相同的子问题, 并且这些子问题能够回到原问题的期望上, 这样就可以找到一个关于这个期望的方程, 直接解了就行了.
这个问题感觉也可以这样做, 因为这个机器人的状态一定最多只有 种, 即每个位置和每个位置上的四个方向, 并且当前的状态仅于上一个状态有关, 所以只要两个状态相同, 他们之后的所有运动轨迹一定也相同. 这样的话根据抽屉原理, 这个机器人的运动状态的循环节长度一定小于 . 我们令初始状态的答案为 , 即起点在 , 两个坐标轴的增量(即方向为) . 只要我们找到状态于状态之间的转移, 就可以列出一个从起点状态回到起点状态的方程, 解出这个方程就行了.
那么我们模拟这个机器人的运动轨迹, 然后考虑转移, 用 表示当前状态, 用 表示下一步的状态. 如果 这个状态扫不到垃圾, 那么一定有:
, 如果 状态可以扫掉垃圾, 那么有 的概率, 直接结束, 这个结果对期望时间的贡献为 .
剩下 的概率, 他扫不到垃圾, 需要转移到下一个状态的期望, 即:
这样一直走下去, 等到 , 就可以列到一个方程.
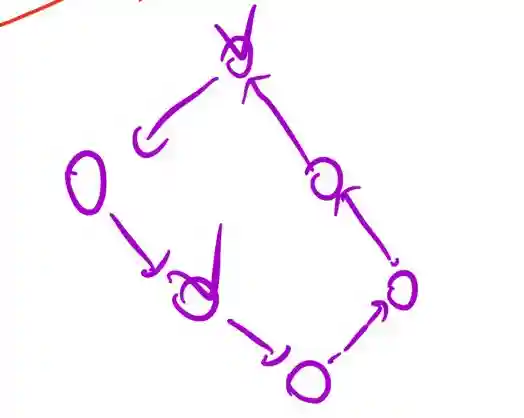
比如这样一个状态转移, 打√的代表可以扫到垃圾.
那么我们可以列出一个这样的方程:
对于初始位置在, 上的这样一个例子, 可以列出方程:

可以看出, 方程全部都是 这样的递归形式, 对于每一个扫到垃圾的状态, 方程会增加一层, 对于扫不到垃圾的状态, 只会让当前层的常数项.
实际上, 对于连续的一堆扫不到垃圾的状态, 他对方程的贡献都是连续的, 变成了一个常数项, 所以可以直接在可以扫到垃圾的时候看一下距离上一次扫到垃圾的时候经过了多少扫不到垃圾的状态, 然后直接把常数项加到方程里.
最后的问题就是如何解这个方程, 这个方程其实直接一层一层解开就行了. 但是可以观察到这个和什么秦九昭算法比较像, 其实就是可以把这个方程展开, 展开成一个多项式的形式, 例如对于倒数第二个样例, 列出的方程为:
左边全部展开, 整理得:
解得 , .
代码:
//
// Created by Orange_Cheers on 2022/1/1.
//
#include <iostream>
#include <algorithm>
#include <vector>
#define MAXN 1005
#define mul(a,b) (((a%mod) * (b%mod))%mod)
#define add(a,b) (((a%mod) + (b%mod))%mod)
using namespace std;
using lovelive = long long int;
const lovelive mod = 1e9+7;
int N, M, stx, sty, edx, edy, P;
lovelive ksm(lovelive a, lovelive k)
{
if(k == 0) return 1;
lovelive ha = ksm(a, k/2);
if(k%2 == 1)
{
return mul(ha,mul(ha, a));
}else{
return mul(ha, ha);
}
}
int main()
{
const lovelive inv100 = ksm(100, mod-2);
cin.tie(nullptr);
ios::sync_with_stdio(false);
int T;
cin >> T;
while(T--)
{
cin >> N >> M >> stx >> sty >> edx >> edy >> P;
int x, y, dx, dy;
x = stx, y = sty, dx = dy = 1;
if(x + dx > N || x+dx < 1) dx *= -1;
if(y + dy > M || y+dy < 1) dy *= -1;
int sdx = dx, sdy = dy;
lovelive cnt = 0;
static vector<lovelive> v;
v.clear();
do{
if(x == edx || y == edy) v.push_back(cnt), cnt = 0;
x += dx;
y += dy;
if(x + dx > N || x+dx < 1) dx *= -1;
if(y + dy > M || y+dy < 1) dy *= -1;
cnt++;
}while(!(x == stx && y == sty && dx == sdx && dy == sdy));
v.push_back(cnt);
lovelive ans = 0;
lovelive np = 1;
for(int i = 0;i < v.size();i++)
{
ans = add(ans, mul(v[i],np));
if(i == v.size()-1)
{
ans = mul(ans, ksm(((1 - np)%mod + mod) %mod, mod-2));
break;
}
np = mul(np, ((1 - mul(P, inv100))%mod + mod) % mod);
}
cout << ans << endl;
}
return 0;
}