求了两下午导, 调了半天代码, 终于验证了我寒假的想法, 自己用softmax回归(我也不知道这个叫什么)实现了MNIST手写数字识别.
寒假里那篇讲Logistic回归的最后, 我按照Logistic回归的想法提出了一种解决多分类问题的方法, 然后想着这玩意不就能识别手写数字了嘛, 但是这学期一直在摸鱼, 没有去尝试写过.
Logistic回归其实还是建立在线性回归上. 线性回归就是拟合出一个矩阵 , 让 尽可能逼近真实答案.
Logistic回归是加了一个非线性函数Sigmoid函数. 他构造的是 , 把输出定义为属于其中一类的概率, 让 尽可能逼近真实答案. 因为Sigmoid函数是可导的, 所以就可以利用链式法则求出 对矩阵中每一项的导数, 即 . 这样就可以找到这个函数在一个点的梯度, 就可以用梯度下降啦.
而在这个基础上, 我们可以让 不再代表一个数, 让他表示一个 的矩阵, 其中 是类别个数, 每一项代表输入处于这一类的概率. 然后还是利用一个可导函数+线性拟合的思路, 让 , 这个函数 需要根据线性拟合的结果(也是一个 的矩阵), 得到这个输入属于每个类的概率.
这个函数首先要保证输出的矩阵每一项加起来为1, 因为输入处于每一类的概率之和一定为1. 还要保证这个函数的输入(即 )越大, 对应的概率也要越大.
我当时提出直接用输入的每一项比上和, 即 来当作这个输入函数. 但是发现还有个叫softmax的东西, 就直接用了softmax, 有时间试试我提出的那个咋样, 肯定不好用, 我就想知道有多不好用.
softmax看名字就知道这是一个soft的max. 为了满足输入越大概率越大, 我们可以直接用一个max函数. 即对于一个 , 直接看哪一项最大就行, 最大的就认为是分类的结果.
但是这样做有两个问题, 一个是直接这样把其他的可能性一棒子打死, 就不给他们翻身的机会. 训练过程中是要不断修改的, 直接认为这次分类的结果是对的, 其他类别都是错的, 就没有了训练的空间. 第二个大问题就是, 这个函数不可导, 也基本没有了训练的方法.
所以softmax就来了:
其实就是先把所有的值来个exp, 然后再用我的那个方法.
这样不仅保证值大的项得到的概率也很大, 而且还能和其他项拉开差距. 最重要的是, 它可导.
那对于手写数字识别这个问题, 我们就可以让, 然后训练就行啦. 就是我预测的这个输入在每一类的概率
然后选Loss函数, 和Logistic回归一样, Loss函数我们选用交叉熵, 交叉熵也在之前的文章讲过啦.
Loss函数:
其中是训练数据的个数, 第二个求和实际上就是求真实数据分布对我的预测分布的交叉熵. 是真实分布的One-hot向量, 即真实在哪一类, 这个向量的哪一项就是1, 其他都是0.
在MNIST手写数字识别里, 矩阵是 的, 和 都是 的, 是一个 的列向量.
其实, 矩阵只有一项是 , 那就可以把交叉熵改成:
是这个数据真实类别.
然后, 为了拟合出 里的 , 需要求出 对 的每一项的偏导, 即.
由链式法则:
下面研究 对 的偏导.
考虑到当 时, , 所以:
其中,
是一个 的列向量.
由矩阵相乘可知,
所以主要看 就行啦.
要求, 首先要讨论一下 和 的关系.
-
时:
-
时:
然后把玩意带回到 里.
最后求出来的结果还是很简单的.
公式推到完啦, 下一步就是写代码.
MNIST数据集谷歌一下就有了:
下下来之后是个二进制文件, 下面介绍了二进制文件的构造.

这是训练集输入, 从第16B开始, 每一个字节代表一个像素, 一张图有784个像素, 一共有60000个图.
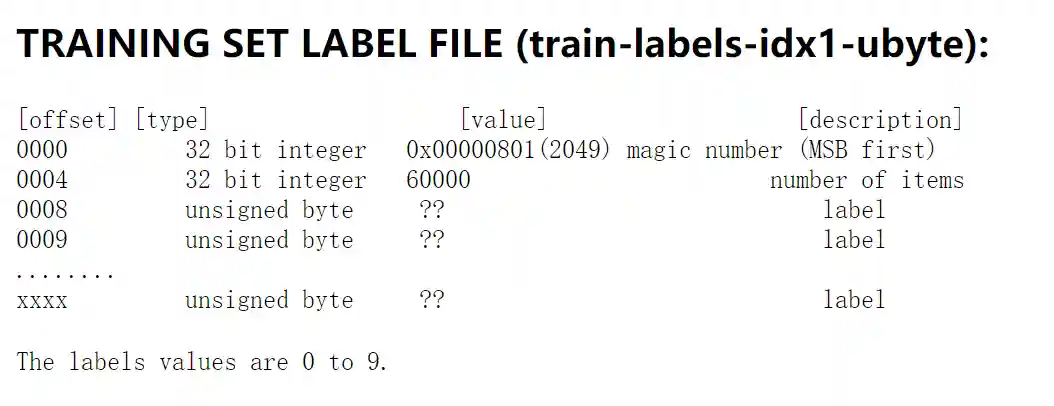
这是训练集输出, 从第8B开始, 每一个字节代表一张图片的标签.
为了验证一下数据是不是这样用的, 我写了个程序把第一个图片搞出来看看长啥样.
把这个输入文件从第16B开始, 读取784B, 生成到一个ppm图片里.
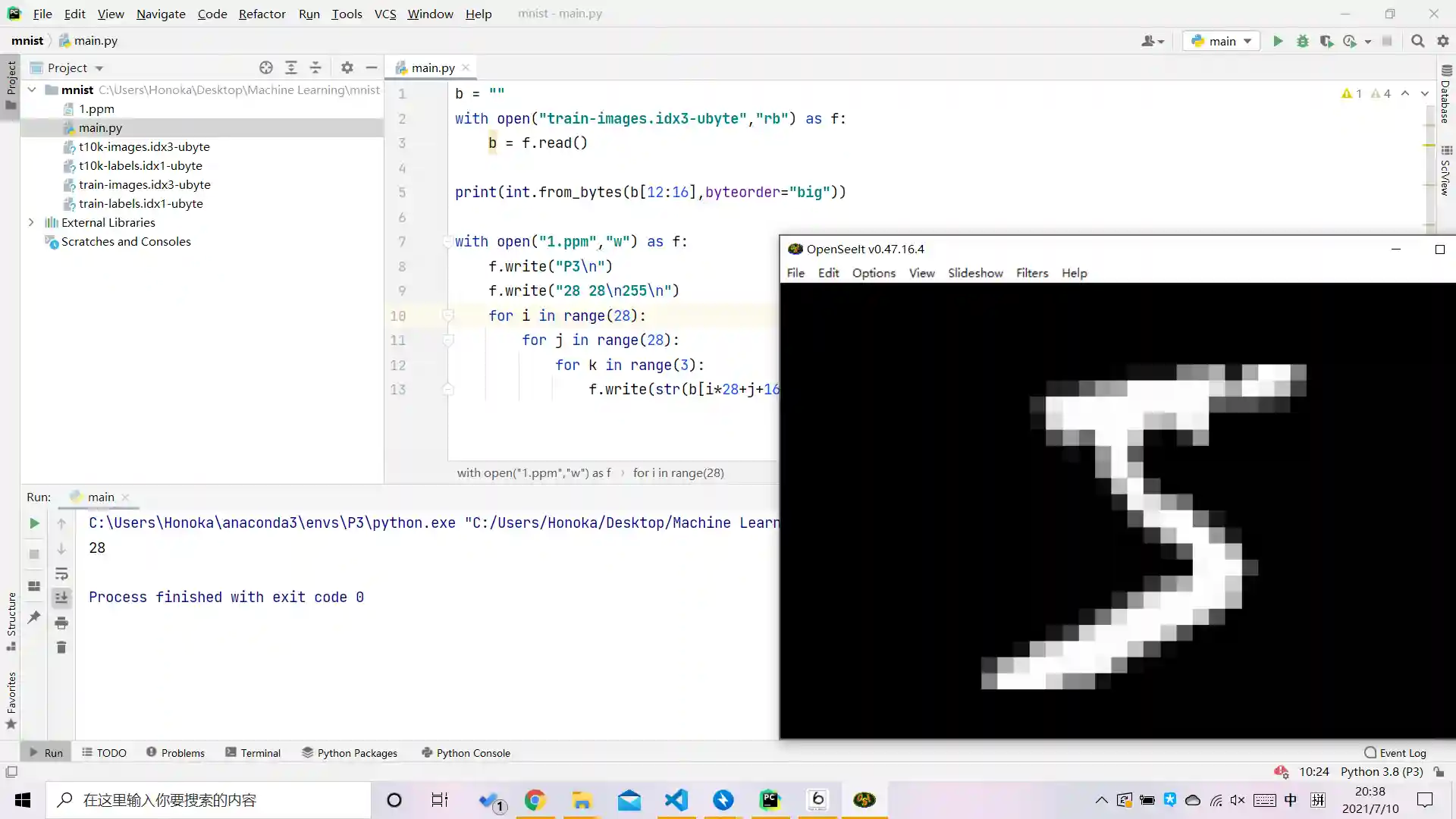
我猜这是个5.
然后按照输出的格式, 读取第8个字节.
果然是个5, 我眼真好使.
除了训练数据, 他还给了测试数据, 只不过测试数据只有10000个.
验证了这些数据集的构造后, 就开始写代码.
第一部分就是读入数据集嘛, 构造一个 的训练输入矩阵. 但是我无论用什么方法, 读入数据都挺慢的. 后来我发现numpy里有个叫fromfile的东西, 可以直接读取这种东西, 速度飞快, 大意了.
然后就是把上面的推导过程写成代码, 代码挺难写的, 而且要注意输入从一个数据变成了60000个数据同时输入, 写了一两小时才写完.
import numpy as np
m = 60000
n = 10000
trainx = np.fromfile(open("train-images.idx3-ubyte"), dtype=np.uint8)[16:].reshape((m, 28 * 28)).T
rawtrainy = np.fromfile(open("train-labels.idx1-ubyte"), dtype=np.uint8)[8:].reshape(m)
testx = np.fromfile(open("t10k-images.idx3-ubyte"), dtype=np.uint8)[16:].reshape((10000, 28 * 28)).T
rawtesty = np.fromfile(open("t10k-labels.idx1-ubyte"), dtype=np.uint8)[8:].reshape(10000)
t = np.ones((10,784))/1000
def softmax(x, s):
y = np.exp(x)
for i in range(s):
y[:,i] = y[:,i] / y[:,i].sum()
return y
def calcP(w):
return softmax(np.dot(w, trainx),m)
def calcPtest(w):
return softmax(np.dot(w, testx),n)
def calcJ(P):
J = 0
for i in range(m):
J = J + np.log(P[rawtrainy[i]][i])
return J / (-m)
def calcJd(w):
P = calcP(w)
print("loss:", calcJ(P))
for i in range(m):
P[rawtrainy[i]][i] -= 1
tt = np.zeros((10,784))
for i in range(m):
tt += np.dot(P[:,i].reshape((10,1)),trainx[:,i].T.reshape(1,784))
#print(trainx[:,1].T.reshape(1,784), P[:,1].reshape((10,1)), np.dot(P[:,1].reshape((10,1)),trainx[:,1].T.reshape(1,784)))
return tt/(m)
learning_rate = 0.000005
def gradient_descent(t):
tt = t - learning_rate * calcJd(t)
# print(tt)
# print(t0,t1,calcJ(tt0,tt1))
return tt
P = calcPtest(t)
tcnt = 0
for i in range(n):
if np.argmax(P[:,i]) == rawtesty[i]:
tcnt = tcnt + 1
print("acc:", tcnt/n)
for i in range(10000):
#print(t)
t = gradient_descent(t)
if i % 10 == 0:
P = calcPtest(t)
tcnt = 0
for j in range(n):
if np.argmax(P[:,j]) == rawtesty[j]:
tcnt = tcnt + 1
print("Epoch",i,"// acc:", tcnt/n)
为了把训练结果表示的更清楚一些, 我每10次迭代都会用测试集测试一下正确率.
调试也调了挺长时间的, 包括调代码的错误, 调学习率之类的.
不过出人意料的是, 这玩意竟然只需要迭代一次就能达到67%的正确率. 当时刚跑出来正确结果我都不信, 因为调了半天, 我都觉得我这辈子调不出来了. 然后我在训练之前用随机的参数矩阵测试了一下正确率, 果然是10%左右, 就说明我的测试正确率的代码没问题, 他的正确率确实只用了一次迭代就达到了67%.
迭代20次时, 正确率已经达到了86%左右, 之后正确率上升的就慢慢缓慢了.
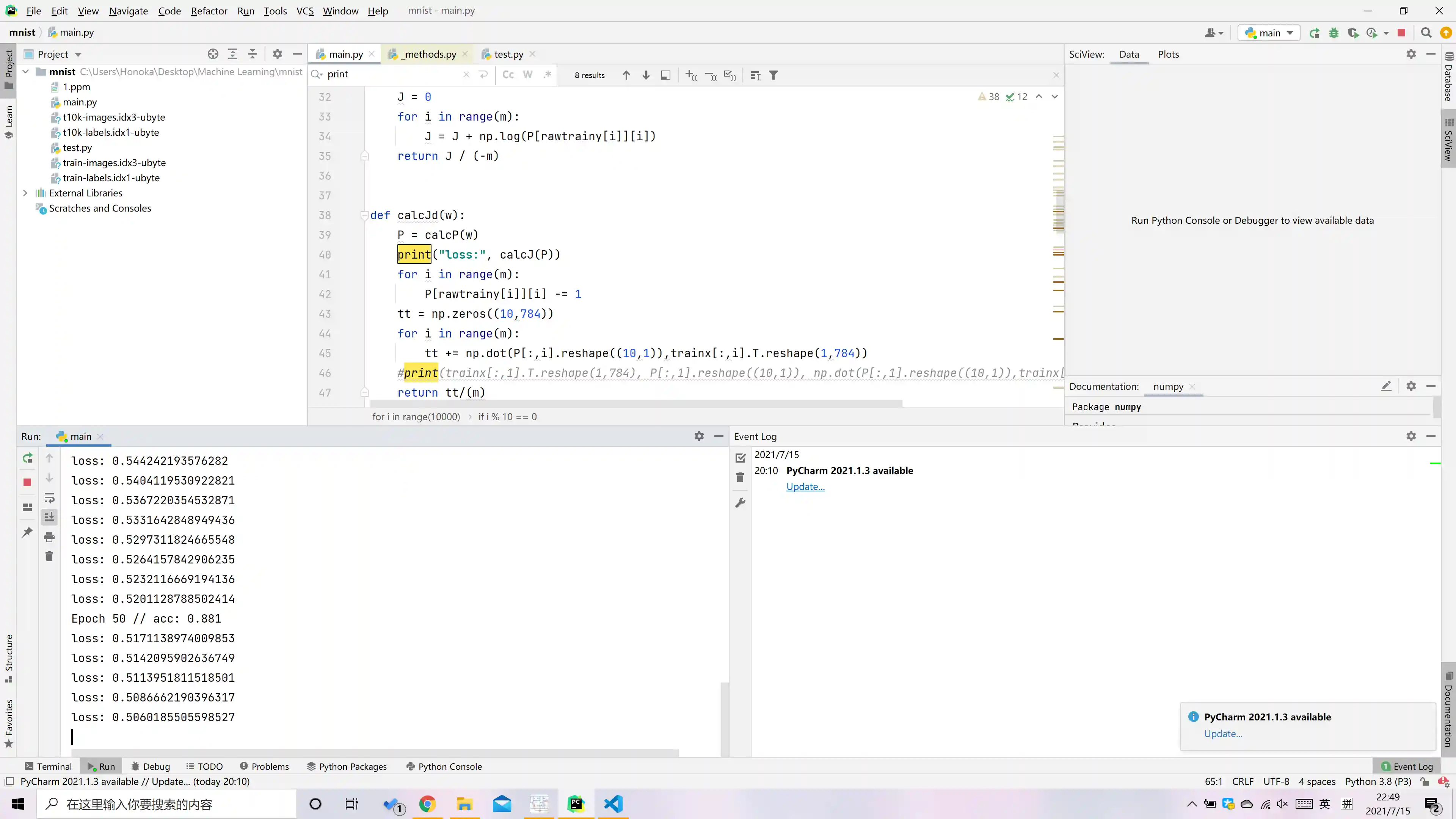
这么简单的方法能达到这么高的正确率是我没想到的, 不愧是机器学习的Hello World.
这个方法其实和一个全连接的神经网络是一样的, 只是我直接写成了矩阵形式.
不怎么参考别人, 自己推公式+自己写程序最后出结果挺快乐的, 感觉自己什么都会, 有点飘了.
下班了, 明天还要去讲课, 这几天好累. 感觉后面应该要学点东西了, 思而不学则殆.
