基础算法
贪心
根据贪心的数学背景我们在做贪心题目的时候一般有两种策略： 1.把一个问题划分成很多子问题，对于每个子问题直接求最优解，然后合成一个最优解； 2.对于当前局面，搜索所有可能的“临近局面”，选择最优的局面进行转移
数据范围较大时，一般使用贪心
贪心的复杂度一般很小
eg1.
按单价排序即可
eg2.
(https://imgchr.com/i/9rw1gI.webp.webp.webp.webp.webp)
数学上的mod指如果mod为负数,不断加模数直到为正数.
即 '5 mod 6 = 5'
eg3-4
紫书区间问题
eg5.
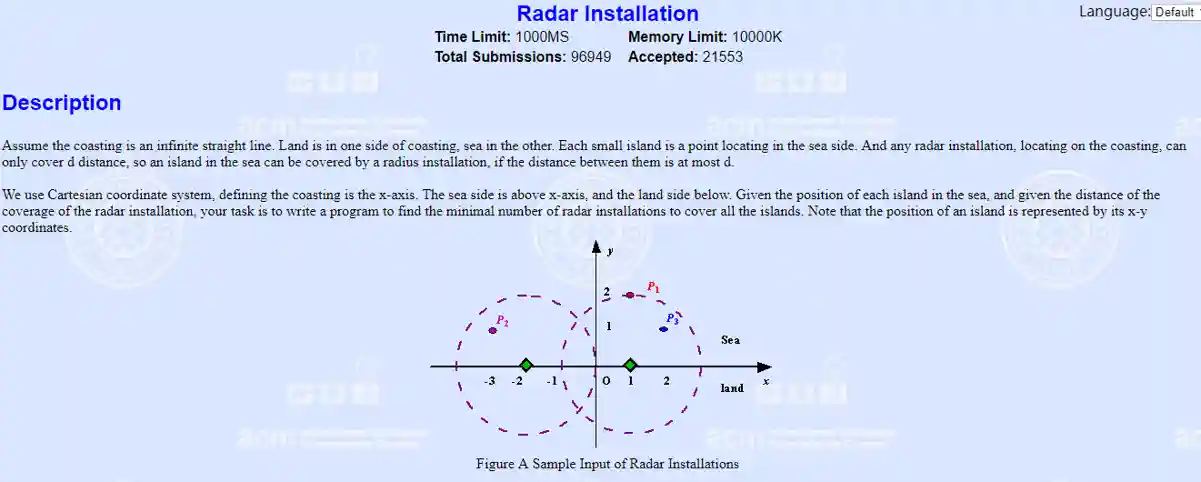非矩形贪心问题一定要转化成线段问题
- 雷达放在x轴上一定比放在x轴下方更优
错误思路
从左到右考虑所有岛,在能探测到一个岛的前提下,尽可能的向右放由于圆的特性,会出现以下反例
正确思路
考虑到圆的复杂,应转化为线段贪心问题.改变研究对象
考虑研究每一个岛屿.
由于雷达的半径固定,所以对于每一个与x轴距离小于半径的岛屿,都能在x轴上找到一个区间,使这个区间里所有的雷达都能探测到这个岛屿.
问题转化为区间选点问题.
eg6.
进制问题
因为1!+2!+...+(n-1)! < n!
所以如果可以表示,则一定可以通过每次取最大的不超过n-已表示的数的数的阶乘得到
[一个我不知道为什么的结论]
eg7.
字典序最大即越靠前越大
当K<= N-1时,把第N个数换到最前
K>N-1时类似.
eg8.
过于复杂先挖个坑
贪心的骗分策略
1.贪心算法与随机化算法的结合（例如模拟退火）
- 在决策时有概率接受比当前情况差的方向
- 在搜索到结果时以一定概率跳出当前解，重新开始贪心
- 在贪心开始的时候，利用随机化选择多个起点开始贪心，取其最小值
可以在最外层循环1000次随机起点来贪心,在数据范围小时极为有效分治
分治的用处
分治算法在OI中的运用主要在两个方面：
- 基于二分查找、三分查找的运用
- 将题目划分为更细小的子问题的运用
二分
- 本质:在一个范围里确定一个分界,使分界的左边满足一个条件,右边满足一个条件
- 适用范围:范围满足单调性
常见使用情景:
- 简单的二分查找
- 在一个单调函数里寻找可行最值
- 最值的最值
首先我们需要一个好的模板
while(l + 1 < r)
{
int mid = (l + r + 1) >> 1;
if(judge(mid))
{
r = mid;
}else{
l = mid;
}
}
if(!judge(l))l = r;
//by Chthollyeg1.
- 借教室的原则是先到先得 这句话点明修改的订单编号满足单调性.即如果前面的订单都满足不了,后面的订单一定不能满足.如果后面的订单可以满足,前面的订单一定能满足.
- 主题框架 既然满足单调性,不难想到二分.二分出能满足的订单与不能满足的订单的分界即可.
- 数据结构 显然这道题多次进行区间修改,单点查询 的操作,考虑用差分来维护.
eg2.
有一个序列{Ai}以及m个区间[li..ri]
你现在可以选择k个区间，对于每个被选中的区间[l..r]，Al~Ar的数都会增加delta
求在所有方案中a中最小值最大为多少- 二分 + 一些神奇的算法
- 这个神奇的算法能计算出能否选中k个区间使任意一个点仍保持在k以下
- 二分出k的最大值即可
- 具体使什么神奇的算法我好像忘了但好像是贪心
eg3.
过于复杂先开个坑
三分
- 使用范围:求一个单峰函数的最值
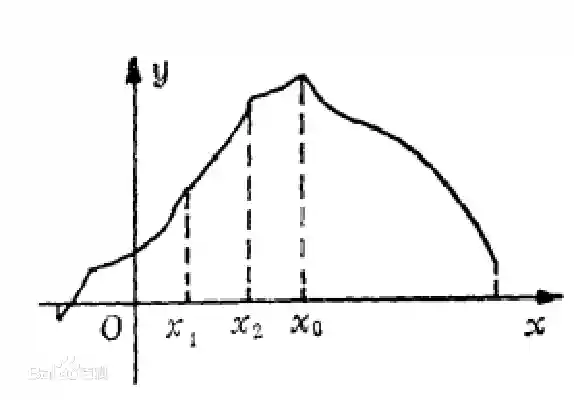
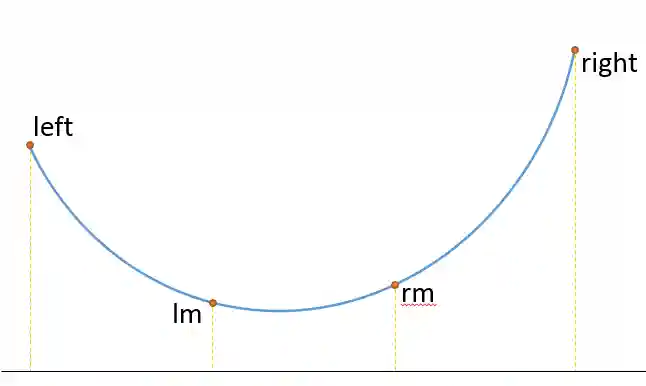
ppt好像有错误不确定就不写了
归并类分治
分块!!!!!
类型
- 给出一个长度为n的数列，以及m个操作，支持区间加法，单点查询
- 给出一个长为n的数列以及m个操作，支持区间加法，并询问区间内小于等于某个数x的元素个数
- 给出一个长为n的数列以及m个操作，支持区间开方，区间求和
分块
分块是线段树/树状数组的一个替代品.
给定一个区间,分为[sqrt(N)]块,每一块有[sqrt(N)]个元素.
剩余的不足[sqrt(N)]个元素单独暴力处理.
[]为向下取整
区间加法,单点查询
类lazy标记
每一块都有一个lazy标记.
加法区间内的整块加法,只需在加lazy标记上加.
查询时加上该块的标记即可.
不在整块内的?暴力啊啊啊啊!
区间加法,查询小于x的个数
每一块排序+二分 不解释
不在整块内的同样暴力啊啊啊
区间开方,区间求和
因为是向下取整开方,所以每一数在开方后多次后就会变为1
然后自己研究吧(狗屎)
eg1.
难点主要在如何求[l,r]之间不同的元素
用pre[i]代表上一次出现a[i]这个元素的位置,问题转化为查询[l,r]区间内pre[i] < l的个数.
O(n)即可完成预处理
2018-2-16